集中趋势/离中趋势
集中趋势
均值:衡量分布比价规律的均匀的连续值
中位数:衡量异常值(最大值最小值)的集中趋势
df.median()众数:衡量离散值的集中趋势
df.mode() #众数可能不是唯一的,返回行数就是众数的数量分位数:把数据从小到大排列后切分成等份的数据点,Q值 计算的是位置
df.quantile(q=0.25) #取四分位数离中趋势(离散程度)
标准差
df.std()方差:数值越大,数据越离散;数值越小,数据越聚拢
df.ver()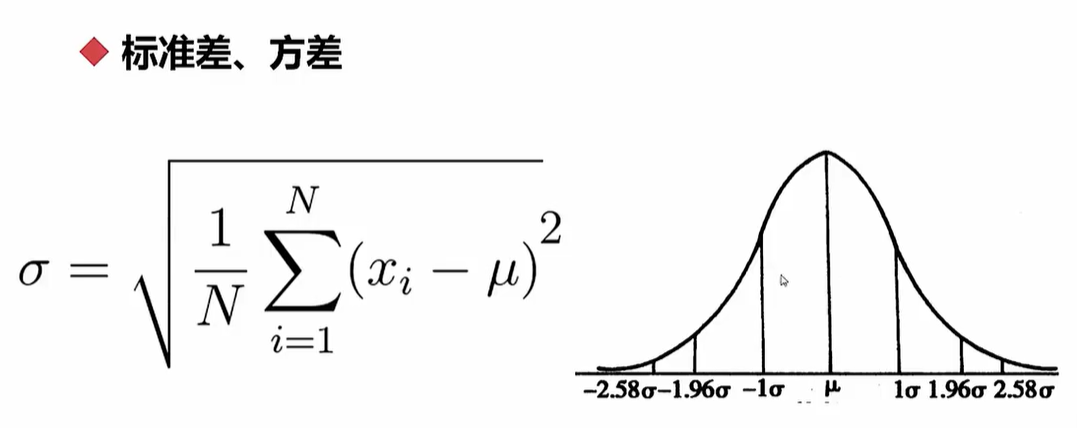
正态分布概率:69%/95%/99%(面积)
数据分布 - 偏态与峰度
偏态系数:数据平均值偏离状态的衡量
df.skew()对称分布的数据,中位数与均值差距不大甚至相等
非对称分布的数据,中位数与均值差距较大,称为有偏态的分布
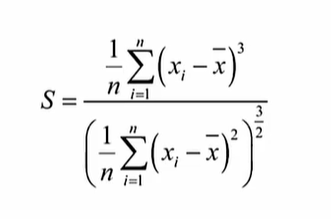
S的值为正数时,是正偏,均值较大
S的值为负数时,是负偏,均值较小
峰态系数:数据分布集中强度的衡量
df.kurt() #以正态分布为0作为标准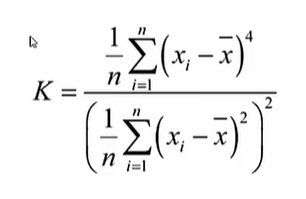
K值越大,数据分布曲线图越尖锐
K值越大,数据分布曲线图越平缓
正态分布的峰态系数一般为3,当峰态系数相差大于2,即K1<1或K1>5时,不是正态分布(可以直接拒绝正态分布的假设)
数据分布 - 分布概率
import scipy.stats as ss # 导入scipy统计包,并重新命名为ss正态分布
ss.norm
ss.norm.stats(moments="mvsk") # m均值,v方差,s偏态系数,k峰态系数
ss.norm.pdf(0.0) #指定分布函数的横坐标,返回相应的纵坐标的值
ss.norm.ppf(0.9) #在标准正态分布中,找到使得累积概率为 90% 的分位点 。输入0-1之间的数,表示累计值。
ss.norm.cdf(2) #从负无穷一直积分到2,累计概率是多少
ss.norm.rvs(size=10) # 得到10个符合正态分布的数字
ss.normaltest() # 正态检验,基于偏态和峰态的检验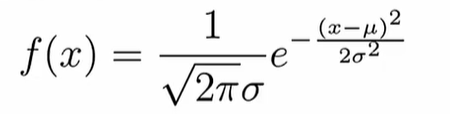
三大分布
卡方分布
ss.chi2 # 表示卡方分布,操作与正态分布一样:pdf\ppf\cdf
ss.chi2_contingeney([x1,y1],[x2,y2]) #卡方检验,返回检验统计量、P值、自由度、理论分布 几个变量都是标准正态分布(均值为0,方差为1),几个标准正态分布的平方和满足的分布,叫卡方分布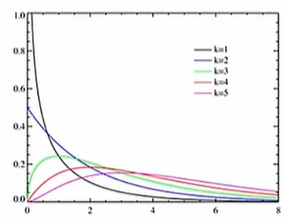
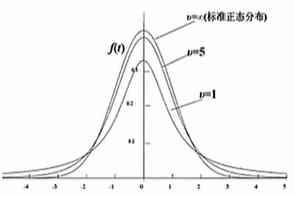
T分布
ss.t # 表示T分布,操作与正态分布一样:pdf\ppf\cdf
ss.ttest_ind(样本1,样本2) # T检验,返回样本统计量和P值,P值大于0.05,接受假设,即均值没有差别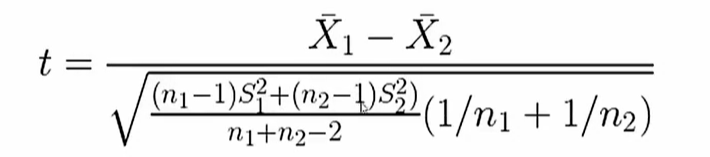
S12表示样本1的方差,n1表示样本1的数量
S22表示样本2的方差,n2表示样本1的数量
正态分布的一个随机变量除以一个服从卡方分布的变量,就是T分布
用来根据小样本来估计成正态分布,且方差未知的均值(两组数据的均值有没有较大差异性)
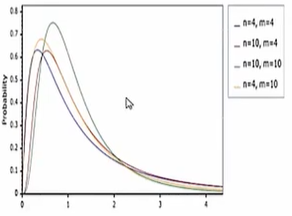
F分布
ss.f # 表示F分布,操作与正态分布一样:pdf\ppf\cdf
ss.f_oneway([样本1],[样本2],[样本3]) #F检验,返回样本统计量和P值构成两个服从卡方分布的随机变量的比(卡方分布的商)
抽样理论
df.sample(n=10) # 从DF中抽取10条记录
df.sample(frac=0.15)# 从DF中抽取百分比的记录完全随机抽样
等差距抽样:根据某属性,从低到高进行排列,等差距的进行抽样
分类的分层抽样:根据各个类别的比例进行抽样,保证样本在某个类别下的分布与整体时一致的
抽样误差与精度

n:抽样的数量
N:整体的数量
方差是整体的方差

Z:标准差的正负距离的倍数(见方差的正态分布图),达保证69%的概率时Z为1,达保证99%的概率时Z为2.58
Δ是需要控制的误差
数据分类
定类(按类别分):根据事物离散、无差别的属性进行分类。如性别、民族等
定序(按顺序分):可以界定数据的大小,但不能测定差值。如高、中、低收入等
定距(按间隔分):可以的界定数据大小的同时,可测定差值,但无绝对零点(乘、除、比率,没有实际意义)。如摄氏温度
定比(按比率分):可以界定数据大小,可测定差值,有绝对零点。如身高、体重、身高、体积等
单属性分析
异常值分析
连续异常值
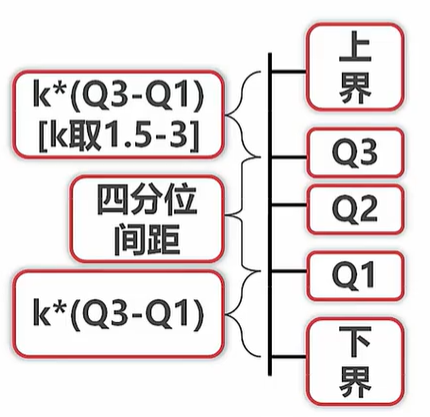
当k取到1.5时,邻近边界的值算中等异常
当k取到3时,邻近边界的值算非常异常
处理方法:1、直接舍弃 2、用边界值代替
离散异常值
离散属性定义范围以外的值均为异常值
处理方法:1、直接舍弃 2、把所有异常值当做一个单独的值来处理,标记出来和正常值区分
知识异常值
在限定知识与常识范围外的所有值均为异常值
如身高大于10m等
对比分析
绝对数与相对数
绝对数比较,如收入,评分,身高
相对数比较,将几个数联合起来构成一个相对数
结构相对数:产品合格率,考试通过率等
比例相对数:总体内用不同部分的数值进行比较
比较相对数:同一时空下,相似或同质的指标进行对比,如不同电商互联网公司的不同待遇水平
动态相对数:如物理上的速度,用户数量的增速
强度相对数:性质不同,但有相互联系的属性进行联合,人均GDP,粮食的亩产,密度等
时间、空间、理论维度比较
时间上:
同比:上一年度同一个月份等进行比较
环比:这一年度不同一个月份的比较
空间上:
城市国家地区;公司的不同部门,不同公司之间
经验与计划:
经验:与历史数据进行对比,如失业率与历史失业率
计划:进度与排期的比较
结构分析 - 各组成部分的分布与规律
静态结构分析:分析总体的组成
动态结构分析:以时间为轴,分析结构变化的趋势
分布分析 - 数据分布频率的显示分析
直接获得的概率分布(不一定都是有意义的,与分析目的有关)
判断正态分布:用假设检验法;偏态的绝对值比较大,就不是正态分布;峰态系数(假设正态分布峰态为3)大于5小于1,就不是正态分布
极大似然:极大似然估计(Maximum Likelihood Estimation, MLE)是一种常用的参数估计方法,基本思想是找到能够使观测数据出现概率最大的参数值作为参数的估计值(最好和已有分布建立联系)
多因子与复合分析
假设检验与方差检验
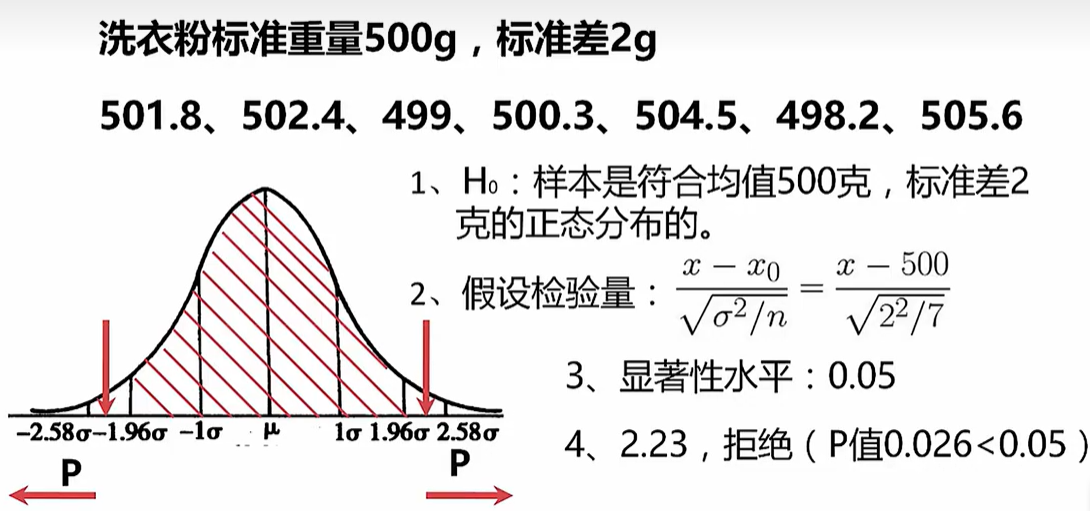
假设检验 - P检验 - 临床药物的效果
根据一定的假设条件,从样本推断总体,或者推断样本与样本之间关系的方法
建立原假设H0(包含等号),H0的反命题为H1,也叫备择假设(一般不符合某分布)
选择检验统计量(使用均值、方差等性质构造的转换函数,目的是为了符合一个已知的的分布)
根据显著性水平(一般为0.05(双边检验),用α表示,是可以接受的假设的失真程度的最大限度,显著性水平与相似度的加和为1。如确定数据有95%的可能是某个分布,那么显著性水平为5%,显著性水平定的越低,对数据和分布契和程度的要求越高),确定拒绝域(确定显著性水平后,已知分布上就可以画出与假设分布相似度比较高的区域,叫做接受域。其他区域叫做拒绝域)
计算p值或者样本统计值,做出判断(方法一:根据区间估计的方法,计算检验统计量的分布区间,看区间是否包含需要比较的分布的特征。方法二:计算P值,和显著性水平进行比较,当计算的P值小于显著性水平,可以判定假设为假)
假设检验 - 卡方检验 - 两因素之间有没有较强的联系
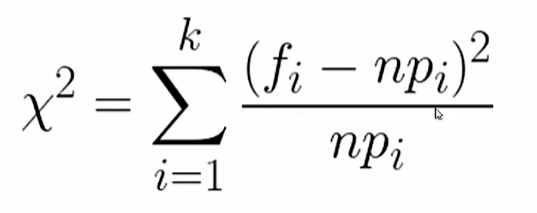
fj表示实际值,npi表示的是理论分布(假设分布)

当卡方值计算出来大于P值对应的卡方值, 就可以拒绝原假设
ss.chi2_contingeney([x1,y1],[x2,y2]) #得到检验统计量、P值、自由度、理论分布卡方检验通常用来检验两因素之间有没有较强的联系
假设检验 - F检验(方差检验) - 多样本两两之间是否有差异
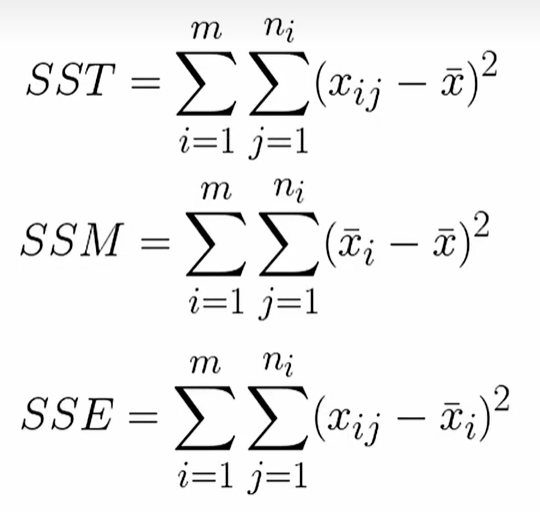
ni:每一组数据的数量,n指的是所有数据的数量
xi:每一组数据的均值,x的均值指的是所有数据的均值
xij:数据本身
SS指的是平方和,SST是总变差平方和,SSM是平均平方和(组间平方和),SSE是残差平方和(组内平方和)

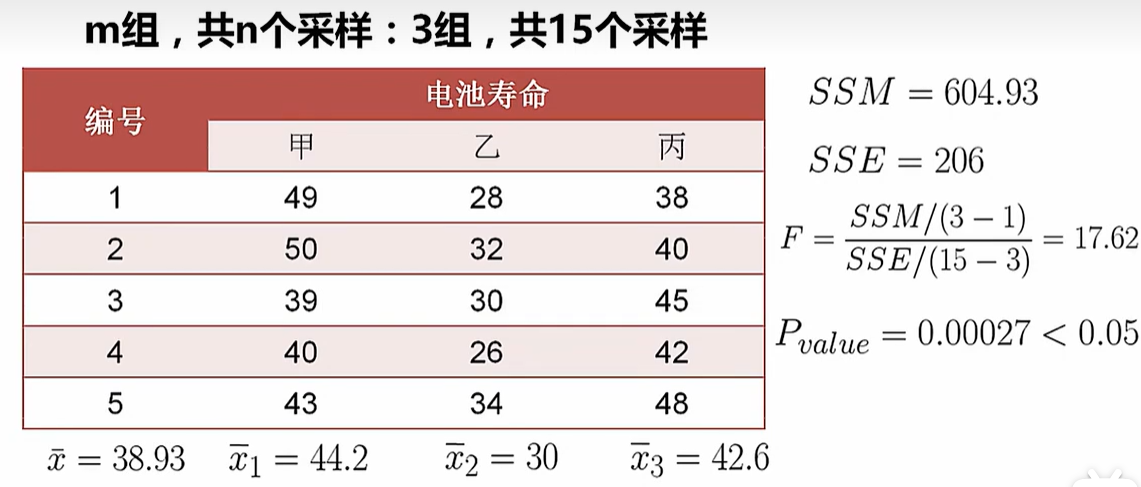
ss.f_oneway([样本1],[样本2],[样本3]) #F检验,返回样本统计量和P值Q-Q图
横轴:正态分布的分位数的值
纵轴:已知分布的分位数的值
得到的散点图,如果和x,y轴的角平分线的的图重合,就是符合正态分布(默认)的
from statsmodels.graphics.api import qqpolt
from matplotlib import pyplot as plt
plt.show(qqplot(样本1))相关系数:皮尔逊、斯皮尔蔓
相关系数是衡量两组数据或者两组样本的分布/变化趋势一致性程度的因子
正相关:相关系数越大越接近与1,两者的变化趋势越正向同步
负相关:相关系数越小越接近与-1,两者的变化趋势越反向同步
不相关:相关系数趋近与0,可以认为两者没有相关关系
Pearson(皮尔逊)相关系数:
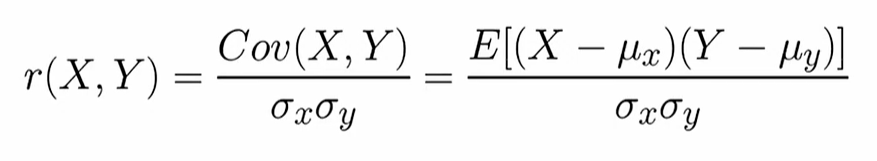
分子:计算了两个变量各自的偏差乘积之和,这实际上是协方差的计算方式,见下图
分母:是各自标准差的乘积,通过这种方式对协方差进行了标准化处理,使得最终得到的相关系数落在-1到+1之间

Spearman(斯皮尔曼)相关系数
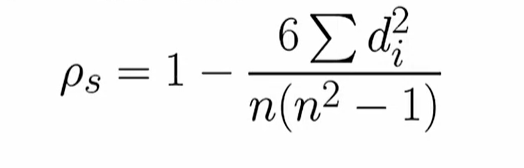
n:每组数据的数量
d:两组数据排名后的名次差(组内排名)
斯皮尔曼和数值没有关系,适合相对比较的情况
实现:
import pandas as pd
s1=pd.Series([样本1])
s2=pd.Series([样本2])
# 方法一
s1.corr(s2) # 返回皮尔逊相关系数
s1.corr(s2.method="spaerman") #返回斯皮尔曼相关系数
# 方法二
df= pd.DateFrame(np.array([s1,s2]).T) # DateFrame针对对列进行计算
df.corr() # 返回皮尔逊相关系数
df.corr(method="spaerman") #返回斯皮尔曼相关系数回归:线性回归
回归:确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法
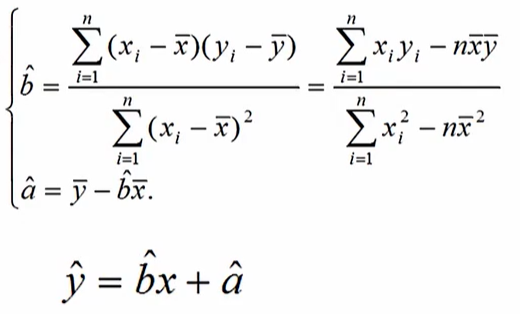
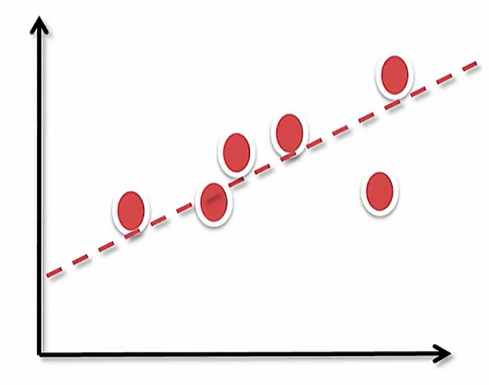
效果判定的两种度量:
决定系数:
越接近于1,回归效果越好;越接近于0,回归效果越差
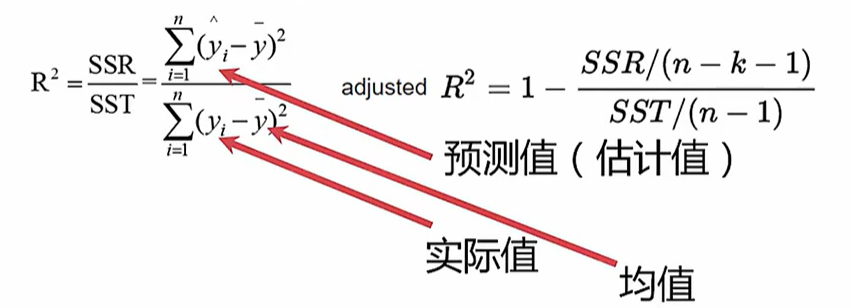
左:一元回归系数的定义
右:多元回归系数的定义(校正式决定系数)
k:参数的个数
残差不相关(DW检验):
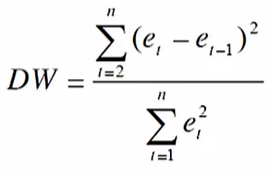
残差e:预测值与实际值的差
将残差值以自变量从小到大排列,套入上述公式得到DW值(0<DW<4)
当DW值为2时,代表残差不相关(好的回归接近2)
当DW值接近于4,代表残差正相关
当DW值接近于0,代表残差负相关
实现:
x=np.arange(10).astype(np.float).reshape((10,1)) # .reshape可以直接改变数组的形状(维度).astype更改数组的数据类型
y=x*3+4+np.random.random(10,1) # .random表示0-1的随机数
from sklearn.linear_model import LinearRegression
reg=LinearRegression() #构建线性回归
res=reg.fit(x,y) #拟合过程
y_pred=reg.predict(x) # 求估计值\预测值
reg.coef_ #参数
reg.intercept_ #截距PCA(主成分)与奇异值分解
线性降维和成分提取
正交变换
主成分分析的流程(降维):

实现:
import pandas as pd
import numpy as np
def myPCA(data,n_components=100000):
# 没有100000维度就全取
mean_vals = np.mean(data,axis=0)
# 对列取均值
mid = data - mean_vals
cov_mat = np.cov(mid,rowvar=False )
# rowvar指定False,对列计算协方差
from scipy import linalg
eig_vals,eig_vects = linalg.eig(np.mat(cov_mat))
# 求协方差矩阵的特征值和特征向量
eig_val_index = np.argsort(eig_vals)
# .argsort得到排序后的索引
eig_val_index = eig_val_index[:-(n_components + 1):-1]
# 取出最大的特征值
eig_vects = eig_vects[:,eig_val_index]
# 取出最大的特征值对应的特征向量
low_dim_mat = np.dot(mid,eig_vects)
# 用矩阵乘法进行计算
return low_dim_mat,eig_vals
# 返回转换后的矩阵\特征,特征值
data=np.array([np.array([样本1]),np.array([样本2])]).T
print(myPCA(data,n_components=1))奇异值分解SVD(PCA方法的一种)

实现:
data=np.array([np.array([样本1]),np.array([样本2])]).T
# array 是 Python 标准库中的一个模块,用于创建高效的数组对象,相比普通的列表(list),它更节省内存,但只能存储同一类型的元素
from sklearn.decomposition import PCA
# sklearn中的PCA算法使用的是奇异值分解法
lower_dim = PAC(n_components=1) #降为一维数据
lower_dim.fit(data) # .fit通过提供的数据来调整模型的参数
lower_dim.explained_variance_ratio_ # 得到维度的重要性
lower_dim.fit_transfrom(data) # 直接得到转化后的数值



评论区